Introduction
Here is the article I wrote last time class.
keita-matsushita.hatenablog.com
Network and Flow

Network is defined as below.
・Network : Graph G(V, E) in which branch capacity Ci(> 0) is defined.
・f(vi, vj) : Branch flow value from vi to vj.
(0 <= f(vi, vj) <= c(vi, vj) : c is a capacity)
And Flow is defined as below
・Flow : f = {f(vi, vj)}
・vs : Source, vt: Sink, F = Flow value
・Flow conservation equation
Outgoing flow - Incoming flow = {F for vs | -F for vt | 0 for else}
Undirected network (無向ネットワーク)
The feature of undirected network is below.
0 <= f(vi, vj) + f(vj, vi) <= c(vi, vj)
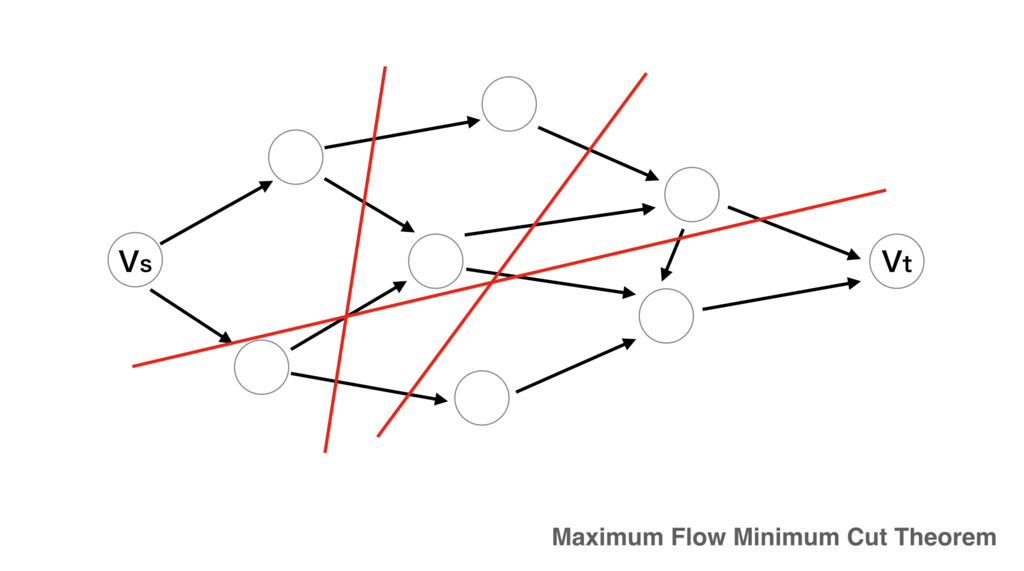
Maximum Flow Minimum Cut Theorem (最大フロー最小カットの定理)

・(X, ~X) : Cut which divides Vs and Vt at X
・Cut capacity c(X, ~X) = Σ(Vi, Vj) (X, ~X)
・Minimum cut (Xo, ~Xo) c(Xo, ~Xo) = min(c(X, ~X))
Maximum Flow Minimum Cut Theorem is defined as below
[ Maximum Flow Minimum Cut Theorem ]
Maximum flow from vs to vt is equal to Minimum cut capacity which divides vs and vt.
Maximum Flow Problem
We can calculate only the value of Maximum flow by using “Maximum Flow Minimum Cut Theorem ”. But we can not calculate the route of the Maximum flow.
This problem can solved by only Heuristic algorithm.
Minimum Cost Flow Problem
・α(vi, vj) : Cost per unit flow of branch (vi, vj) ・Problem
Total cost = Σ α(vi, vj) f(vi, vj) → Minimum

[ Theorem ]
The necessary and sufficient condition of minimum cost flow is that here are no loops with negative cost.
