Introduction
Here is the article of the last time class.
keita-matsushita.hatenablog.com
Matrix Expression of Graphs and Paths
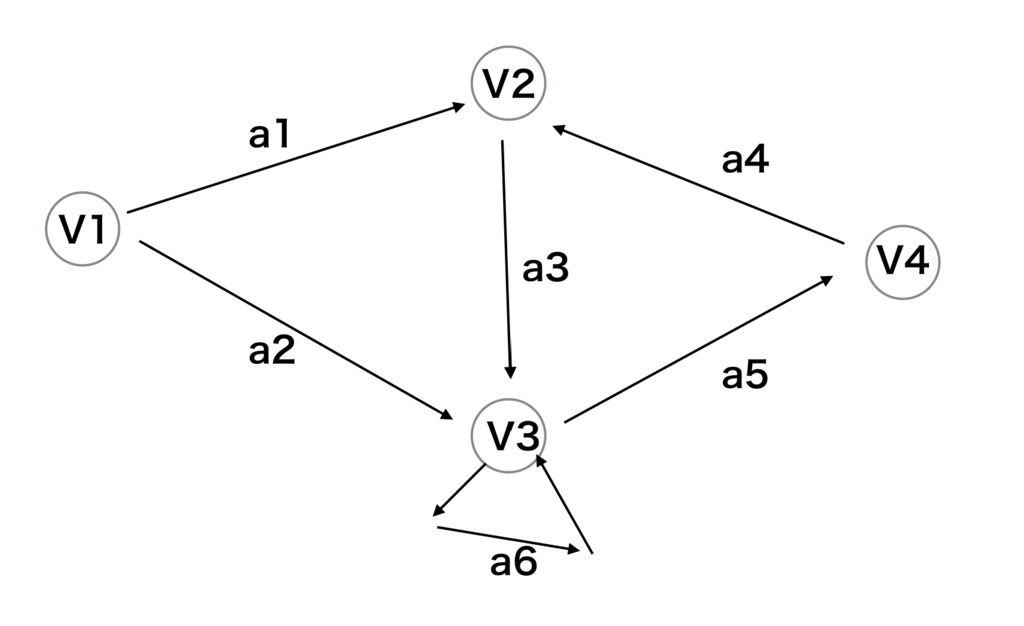
Graphs can be expressed by matrixes. Below matrixes express above the graph.
Incidence matrix (接続行列)
Cols represents branches and rows represents nodes.
+1 means that the node has outdegree from the node and -1 means that the node has indegree from the node.
Path matrix (経路行列)
Cols represents branches and row represents path.
So in above matrix means that the first path is through a1, a3 and a5.
Adjacency matrix (隣接行列)
Both cols and rows represent nodes. 1 means that there is a branch between the nodes.
Adjacency matrix can express the loop of V3 node. So this matrix is very useful.
Adjacency matrix has an important theorem.
[ Theorem ]
The element of Al represents the number of paths withlbranches.
In A2 matrix, the matrix has 2 in 0th row and 2nd col. This means that There are two paths from V1 to V3 with two hops. The one path is through a1 and a3. another paths is through a2 and a6. The both paths hops with 2 branches. In A3 matrix case, the number of hops become 3 as well. So, the index of power corresponds with the number of hops.
Search for Shortest Path
The distance in graph can define as below.
Distance: Sum of the length of the branch of a path
Distance graph (距離網): Graph in which distance is defined
Shortest path tree
Below graph G, T is the shortest path tree from V0 to V1, V2, V3, and V4
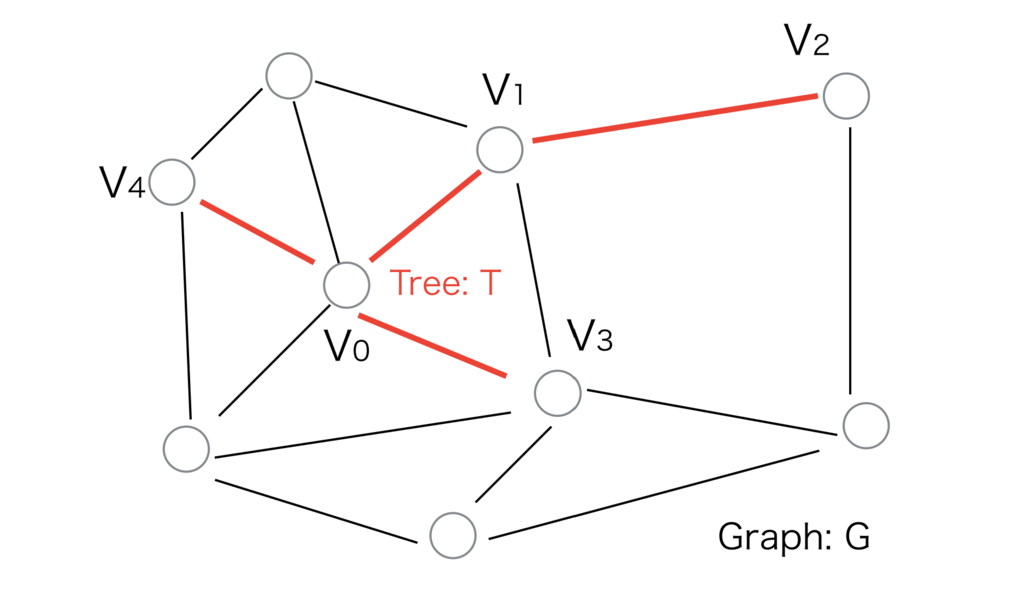
If T covers G, the T is called Maximum shortest path tree.
Search methods of shortest path
We want to know the shortest path in graphs whose branch have distance. The distances are not just 1. Any number can be the distance of the branches. So we can not find the shortest path by just counting the number of branches between the nodes.
There are some methods to find the shortest path
- Heuristic method
- Dijkstra Algorithm
